Regresi logistik adalah bagian dari analisis regresi yang digunakan ketika variabel dependen (respon) merupakan variabel dikotomi. Variabel dikotomi biasanya hanya terdiri atas dua nilai, yang mewakili kemunculan atau tidak adanya suatu kejadian yang biasanya diberi angka 0 atau 1.Tidak seperti regresi linier biasa, regresi logistik tidak mengasumsikan hubungan antara variabel independen dan dependen secara linier. Regresi logistik merupakan regresi non linier dimana model yang ditentukan akan mengikuti pola kurva seperti gambar di bawah ini.
Model yang digunakan pada regresi logistik adalah:Log (P / 1 – p) = β0 + β1X1 + β2X2 + …. + βkXk
Dimana p adalah kemungkinan bahwa Y = 1, dan X1, X2, X3 adalah variabel independen, dan b adalah koefisien regresi.
Regresi logistik akan membentuk variabel prediktor/respon (log (p/(1-p)) yang merupakan kombinasi linier dari variabel independen. Nilai variabel prediktor ini kemudian ditransformasikan menjadi probabilitas dengan fungsi
logit.
Regresi logistik juga menghasilkan rasio peluang (
odds ratios) terkait dengan nilai setiap prediktor. Peluang (
odds) dari suatu kejadian diartikan sebagai probabilitas hasil yang muncul yang dibagi dengan probabilitas suatu kejadian tidak terjadi. Secara umum, rasio peluang (
odds ratios) merupakan sekumpulan peluang yang dibagi oleh peluang lainnya. Rasio peluang bagi prediktor diartikan sebagai jumlah relatif dimana peluang hasil meningkat (rasio peluang > 1) atau turun (rasio peluang < 1) ketika nilai variabel prediktor meningkat sebesar 1 unit.Lebih jelasnya kita dapat mengikuti
ilustrasi berikut ini:
Jika kita ingin mengetahui pembelian kosmetik merk tertentu oleh beberapa orang wanita dengan beberapa variabel penjelas antara lain adalah umur, tingkat pendapatan (low, medium, high), dan status (M – menikah; S untuk single). Pada data tersebut, pembelian merupakan variabel prediktor yang dijelaskan dengan angka 1 sebagai membeli dan 0 sebagai tidak membeli.
1. Dengan SPSS 17.0 data yang diinput dapat berupa:
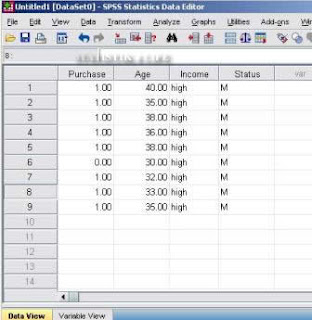
2. Setelah data diinput, pilih Analyze – Regression – Binary logistic seperti berikut:
3. Setelah muncul kotak dialog logistic regression, masukkan variabel dependen purchase ke kolom dependent, dan ketiga variabel independen ke dalam kolom covariates, lalu pilih tombol categoricaluntuk memasukkan variabel kategorik yaitu pendapatan dan status – klik continue:
4. Setelah itu pilih option, checklist classification plot dan Hosmer-lemeshow goodness of fit, kemudian continue:
5. Kemudian pada method pilih enter, kemudian klik OK:
6. Output yang didapatkan adalah sebagai berikut:
Output Case Processing Summary menghilangkan variabel yang tidak diperhitungkan dalam model.
Output classification table diatas menjelaskan bahwa persentase variabel yang diprediksi sebesar88,9 persen adalah baik, dan dari perbandingan antara kedua nilai mengindikasikan tidak terdapatnya masalah homoskedastisitas (asumsi model logit).Pada output variables in equation signifikansi adalah 0,05 artinya model tidak signifikan dan dengan demikian terima H0.
Pada output omnibus test menyatakan bahwa hasil uji chi-square goodness of fit lebih kecil dari 0,05, ini mengindikasikan bahwa model adalah signifikan.Hasil output pada Cox-Snell R2 dan Nagelkerke R memiliki analogi sama dengan nilai R-square padaregresi linier, menyakatan bahwa sebanyak 50,2 persen keragaman dapat dijelaskan oleh model, sedangkan sisanya diluar model.Hasil pada output Hosmer and Lemeshow Goodness-of-Fit Test mengindikasikan bahwa kita dapat menerima H0 karena Lebih dari 0,05 (1 > 0,05).
output variables in the equation menunjukkan nilai signifikansi berdasarkan Wald Statistic, jika model signifikan, maka nilai sig. adalah kurang dari 0,05.Kolom Exp(B) menunjukkan nilai odds ratio yang dihasilkan. Nilai odds ratio yang hanya mendekati 1,0 mengindikasikan bahwa variabel independen tidak mempengaruhi variabel dependen.
Output classplot diatas menunjukkan prediksi pada regresi logistik. Sumbu X menujukkan probabilitas yang diprediksi, sedangkan sumbu Y menunjukkan jumlah kasus yang diamati.

